Cython for NumPy users¶
Note
This page uses two different syntax variants:
Cython specific
cdefsyntax, which was designed to make type declarations concise and easily readable from a C/C++ perspective.Pure Python syntax which allows static Cython type declarations in pure Python code, following PEP-484 type hints and PEP 526 variable annotations.
To make use of C data types in Python syntax, you need to import the special
cythonmodule in the Python module that you want to compile, e.g.import cython
If you use the pure Python syntax we strongly recommend you use a recent Cython 3 release, since significant improvements have been made here compared to the 0.29.x releases.
This tutorial is aimed at NumPy users who have no experience with Cython at all. If you have some knowledge of Cython you may want to skip to the ‘’Efficient indexing’’ section.
The main scenario considered is NumPy end-use rather than NumPy/SciPy development. The reason is that Cython is not (yet) able to support functions that are generic with respect to the number of dimensions in a high-level fashion. This restriction is much more severe for SciPy development than more specific, “end-user” functions. See the last section for more information on this.
The style of this tutorial will not fit everybody, so you can also consider:
Kurt Smith’s video tutorial of Cython at SciPy 2015. The slides and notebooks of this talk are on github.
Basic Cython documentation (see Cython front page).
Cython at a glance¶
Cython is a compiler which compiles Python-like code files to C code. Still, ‘’Cython is not a Python to C translator’’. That is, it doesn’t take your full program and “turn it into C” – rather, the result makes full use of the Python runtime environment. A way of looking at it may be that your code is still Python in that it runs within the Python runtime environment, but rather than compiling to interpreted Python bytecode one compiles to native machine code (but with the addition of extra syntax for easy embedding of faster C-like code).
This has two important consequences:
Speed. How much depends very much on the program involved though. Typical Python numerical programs would tend to gain very little as most time is spent in lower-level C that is used in a high-level fashion. However for-loop-style programs can gain many orders of magnitude, when typing information is added (and is so made possible as a realistic alternative).
Easy calling into C code. One of Cython’s purposes is to allow easy wrapping of C libraries. When writing code in Cython you can call into C code as easily as into Python code.
Very few Python constructs are not yet supported, though making Cython compile all Python code is a stated goal, you can see the differences with Python in limitations.
Your Cython environment¶
Using Cython consists of these steps:
Write a
.pyxsource fileRun the Cython compiler to generate a C file
Run a C compiler to generate a compiled library
Run the Python interpreter and ask it to import the module
However there are several options to automate these steps:
The SAGE mathematics software system provides excellent support for using Cython and NumPy from an interactive command line or through a notebook interface (like Maple/Mathematica). See this documentation.
Cython can be used as an extension within a Jupyter notebook, making it easy to compile and use Cython code with just a
%%cythonat the top of a cell. For more information see Using the Jupyter Notebook.A version of pyximport is shipped with Cython, so that you can import pyx-files dynamically into Python and have them compiled automatically (See Compiling with pyximport).
Cython supports setuptools so that you can very easily create build scripts which automate the process, this is the preferred method for Cython implemented libraries and packages. See Basic setup.py.
Manual compilation (see below)
Note
If using another interactive command line environment than SAGE, like IPython or Python itself, it is important that you restart the process when you recompile the module. It is not enough to issue an “import” statement again.
Installation¶
If you already have a C compiler, just do:
pip install Cython
otherwise, see the installation page.
As of this writing SAGE comes with an older release of Cython than required for this tutorial. So if using SAGE you should download the newest Cython and then execute :
$ cd path/to/cython-distro
$ path-to-sage/sage -python setup.py install
This will install the newest Cython into SAGE.
Compilation¶
Manual compilation¶
As it is always important to know what is going on, I’ll describe the manual method here. First Cython is run:
$ cython yourmod.pyx
This creates yourmod.c which is the C source for a Python extension
module. A useful additional switch is -a which will generate a document
yourmod.html) that shows which Cython code translates to which C code
line by line.
Then we compile the C file. This may vary according to your system, but the C file should be built like Python was built. Python documentation for writing extensions should have some details. On Linux this often means something like:
$ gcc -shared -pthread -fPIC -fwrapv -O2 -Wall -fno-strict-aliasing -I/usr/include/python2.7 -o yourmod.so yourmod.c
gcc should have access to the NumPy C header files so if they are not
installed at /usr/include/numpy or similar you may need to pass another
option for those. You only need to provide the NumPy headers if you write:
cimport numpy
in your Cython code.
This creates yourmod.so in the same directory, which is importable by
Python by using a normal import yourmod statement.
Compilation using setuptools¶
Setuptools allows us to create setup.py file to automate compilation of both Cython files and generated C files.:
from setuptools import Extension, setup
from Cython.Build import cythonize
import numpy
extensions = [
Extension("*", ["*.pyx"],
include_dirs=[numpy.get_include()]),
]
setup(
name="My hello app",
ext_modules=cythonize(extensions),
)
The path to the NumPy headers is passed to the C compiler via the include_dirs=[numpy.get_include()] parameter.
Note
Using memoryviews or importing NumPy with import numpy does not mean that
you have to add the path to NumPy include files. You need to add this path only
if you use cimport numpy.
Despite this, you may still get warnings like the following from the compiler, because Cython is not disabling the usage of the old deprecated Numpy API:
.../include/numpy/npy_1_7_deprecated_api.h:15:2: warning: #warning "Using deprecated NumPy API, disable it by " "#defining NPY_NO_DEPRECATED_API NPY_1_7_API_VERSION" [-Wcpp]
In Cython 3.0, you can get rid of this warning by defining the C macro
NPY_NO_DEPRECATED_API as NPY_1_7_API_VERSION
in your build, e.g.:
# distutils: define_macros=NPY_NO_DEPRECATED_API=NPY_1_7_API_VERSION
or (see below):
Extension(
...,
define_macros=[("NPY_NO_DEPRECATED_API", "NPY_1_7_API_VERSION")],
)
With older Cython releases, setting this macro will fail the C compilation, because Cython generates code that uses this deprecated C-API. However, the warning has no negative effects even in recent NumPy versions. You can ignore it until you (or your library’s users) switch to a newer NumPy version that removes this long deprecated API, in which case you also need to use Cython 3.0 or later. Thus, the earlier you switch to Cython 3.0, the better for your users.
The first Cython program¶
You can easily execute the code of this tutorial by downloading the Jupyter notebook.
The code below does the equivalent of this function in numpy:
def compute_np(array_1, array_2, a, b, c):
return np.clip(array_1, 2, 10) * a + array_2 * b + c
We’ll say that array_1 and array_2 are 2D NumPy arrays of integer type and
a, b and c are three Python integers.
This function uses NumPy and is already really fast, so it might be a bit overkill to do it again with Cython. This is for demonstration purposes. Nonetheless, we will show that we achieve a better speed and memory efficiency than NumPy at the cost of more verbosity.
This code computes the function with the loops over the two dimensions being unrolled.
It is both valid Python and valid Cython code. I’ll refer to it as both
compute_py.py for the Python version and compute_cy.pyx for the
Cython version – Cython uses .pyx as its file suffix (but it can also compile
.py files).
import numpy as np
def clip(a, min_value, max_value):
return min(max(a, min_value), max_value)
def compute(array_1, array_2, a, b, c):
"""
This function must implement the formula
np.clip(array_1, 2, 10) * a + array_2 * b + c
array_1 and array_2 are 2D.
"""
x_max = array_1.shape[0]
y_max = array_1.shape[1]
assert array_1.shape == array_2.shape
result = np.zeros((x_max, y_max), dtype=array_1.dtype)
for x in range(x_max):
for y in range(y_max):
tmp = clip(array_1[x, y], 2, 10)
tmp = tmp * a + array_2[x, y] * b
result[x, y] = tmp + c
return result
This should be compiled to produce compute_cy.so for Linux systems
(on Windows systems, this will be a .pyd file). We
run a Python session to test both the Python version (imported from
.py-file) and the compiled Cython module.
In [1]: import numpy as np
In [2]: array_1 = np.random.uniform(0, 1000, size=(3000, 2000)).astype(np.intc)
In [3]: array_2 = np.random.uniform(0, 1000, size=(3000, 2000)).astype(np.intc)
In [4]: a = 4
In [5]: b = 3
In [6]: c = 9
In [7]: def compute_np(array_1, array_2, a, b, c):
...: return np.clip(array_1, 2, 10) * a + array_2 * b + c
In [8]: %timeit compute_np(array_1, array_2, a, b, c)
103 ms ± 4.16 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)
In [9]: import compute_py
In [10]: compute_py.compute(array_1, array_2, a, b, c)
1min 10s ± 844 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)
In [11]: import compute_cy
In [12]: compute_cy.compute(array_1, array_2, a, b, c)
56.5 s ± 587 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)
There’s not such a huge difference yet; because the C code still does exactly what the Python interpreter does (meaning, for instance, that a new object is allocated for each number used).
You can look at the Python interaction and the generated C
code by using -a when calling Cython from the command
line, %%cython -a when using a Jupyter Notebook, or by using
cythonize('compute_cy.pyx', annotate=True) when using a setup.py.
Look at the generated html file and see what
is needed for even the simplest statements. You get the point quickly. We need
to give Cython more information; we need to add types.
Adding types¶
To add types we use custom Cython syntax, so we are now breaking Python source compatibility. Read the comments!
import numpy as np
import cython
# We now need to fix a datatype for our arrays. I've used the variable
# DTYPE for this, which is assigned to the usual NumPy runtime
# type info object.
DTYPE = np.intc
# @cython.cfunc means here that this function is a plain C function (so faster).
# To get all the benefits, we type the arguments and the return value.
@cython.exceptval(check=False)
@cython.cfunc
def clip(a: cython.int, min_value: cython.int, max_value: cython.int) -> cython.int:
return min(max(a, min_value), max_value)
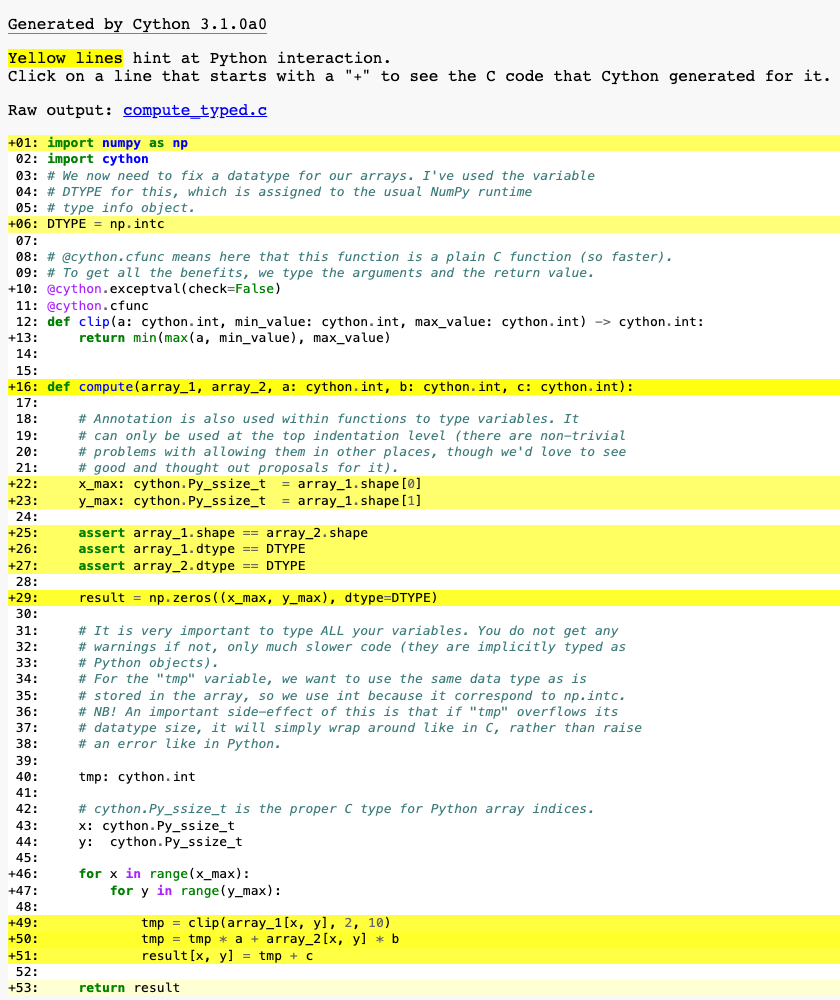
def compute(array_1, array_2, a: cython.int, b: cython.int, c: cython.int):
# Annotation is also used within functions to type variables. It
# can only be used at the top indentation level (there are non-trivial
# problems with allowing them in other places, though we'd love to see
# good and thought out proposals for it).
x_max: cython.Py_ssize_t = array_1.shape[0]
y_max: cython.Py_ssize_t = array_1.shape[1]
assert array_1.shape == array_2.shape
assert array_1.dtype == DTYPE
assert array_2.dtype == DTYPE
result = np.zeros((x_max, y_max), dtype=DTYPE)
# It is very important to type ALL your variables. You do not get any
# warnings if not, only much slower code (they are implicitly typed as
# Python objects).
# For the "tmp" variable, we want to use the same data type as is
# stored in the array, so we use int because it correspond to np.intc.
# NB! An important side-effect of this is that if "tmp" overflows its
# datatype size, it will simply wrap around like in C, rather than raise
# an error like in Python.
tmp: cython.int
# cython.Py_ssize_t is the proper C type for Python array indices.
x: cython.Py_ssize_t
y: cython.Py_ssize_t
for x in range(x_max):
for y in range(y_max):
tmp = clip(array_1[x, y], 2, 10)
tmp = tmp * a + array_2[x, y] * b
result[x, y] = tmp + c
return result
import numpy as np
# We now need to fix a datatype for our arrays. I've used the variable
# DTYPE for this, which is assigned to the usual NumPy runtime
# type info object.
DTYPE = np.intc
# cdef means here that this function is a plain C function (so faster).
# To get all the benefits, we type the arguments and the return value.
cdef int clip(int a, int min_value, int max_value):
return min(max(a, min_value), max_value)
def compute(array_1, array_2, int a, int b, int c):
# The "cdef" keyword is also used within functions to type variables. It
# can only be used at the top indentation level (there are non-trivial
# problems with allowing them in other places, though we'd love to see
# good and thought out proposals for it).
cdef Py_ssize_t x_max = array_1.shape[0]
cdef Py_ssize_t y_max = array_1.shape[1]
assert array_1.shape == array_2.shape
assert array_1.dtype == DTYPE
assert array_2.dtype == DTYPE
result = np.zeros((x_max, y_max), dtype=DTYPE)
# It is very important to type ALL your variables. You do not get any
# warnings if not, only much slower code (they are implicitly typed as
# Python objects).
# For the "tmp" variable, we want to use the same data type as is
# stored in the array, so we use int because it correspond to np.intc.
# NB! An important side-effect of this is that if "tmp" overflows its
# datatype size, it will simply wrap around like in C, rather than raise
# an error like in Python.
cdef int tmp
# Py_ssize_t is the proper C type for Python array indices.
cdef Py_ssize_t x, y
for x in range(x_max):
for y in range(y_max):
tmp = clip(array_1[x, y], 2, 10)
tmp = tmp * a + array_2[x, y] * b
result[x, y] = tmp + c
return result
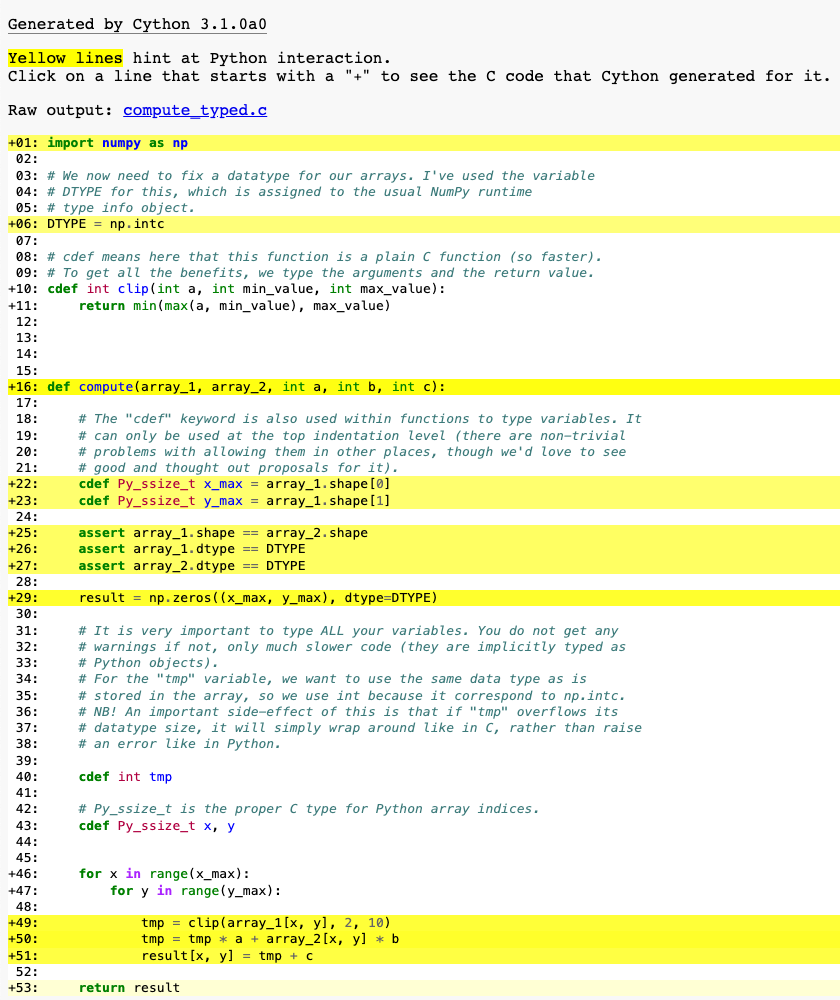
At this point, have a look at the generated C code for compute_cy.pyx and
compute_typed.pyx. Click on the lines to expand them and see corresponding C.
Especially have a look at the for-loops: In compute_cy.c, these are ~20 lines
of C code to set up while in compute_typed.c a normal C for loop is used.
After building this and continuing my (very informal) benchmarks, I get:
In [13]: %timeit compute_typed.compute(array_1, array_2, a, b, c)
26.5 s ± 422 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)
So adding types does make the code faster, but nowhere near the speed of NumPy?
What happened is that most of the time spend in this code is spent in the following lines, and those lines are slower to execute than in pure Python:
tmp = clip(array_1[x, y], 2, 10)
tmp = tmp * a + array_2[x, y] * b
result[x, y] = tmp + c
So what made those line so much slower than in the pure Python version?
array_1 and array_2 are still NumPy arrays, so Python objects, and expect
Python integers as indexes. Here we pass C int values. So every time
Cython reaches this line, it has to convert all the C integers to Python
int objects. Since this line is called very often, it outweighs the speed
benefits of the pure C loops that were created from the range() earlier.
Furthermore, tmp * a + array_2[x, y] * b returns a Python integer
and tmp is a C integer, so Cython has to do type conversions again.
In the end those types conversions add up. And made our computation really
slow. But this problem can be solved easily by using memoryviews.
Efficient indexing with memoryviews¶
There are still two bottlenecks that degrade the performance, and that is the array lookups
and assignments, as well as C/Python types conversion.
The []-operator still uses full Python operations –
what we would like to do instead is to access the data buffer directly at C
speed.
What we need to do then is to type the contents of the ndarray objects.
We do this with a memoryview. There is a page in the Cython documentation dedicated to it.
In short, memoryviews are C structures that can hold a pointer to the data of a NumPy array and all the necessary buffer metadata to provide efficient and safe access: dimensions, strides, item size, item type information, etc… They also support slices, so they work even if the NumPy array isn’t contiguous in memory. They can be indexed by C integers, thus allowing fast access to the NumPy array data.
Here is how to declare a memoryview of integers:
foo: cython.int [:] # 1D memoryview
foo: cython.int [:, :] # 2D memoryview
foo: cython.int [:, :, :] # 3D memoryview
... # You get the idea.
cdef int [:] foo # 1D memoryview
cdef int [:, :] foo # 2D memoryview
cdef int [:, :, :] foo # 3D memoryview
... # You get the idea.
No data is copied from the NumPy array to the memoryview in our example.
As the name implies, it is only a “view” of the memory. So we can use the
view result_view for efficient indexing and at the end return the real NumPy
array result that holds the data that we operated on.
Here is how to use them in our code:
import numpy as np
import cython
DTYPE = np.intc
@cython.cfunc
def clip(a: cython.int, min_value: cython.int, max_value: cython.int) -> cython.int:
return min(max(a, min_value), max_value)
def compute(array_1: cython.int[:, :], array_2: cython.int[:, :],
a: cython.int, b: cython.int, c: cython.int):
x_max: cython.Py_ssize_t = array_1.shape[0]
y_max: cython.Py_ssize_t = array_1.shape[1]
# array_1.shape is now a C array, no it's not possible
# to compare it simply by using == without a for-loop.
# To be able to compare it to array_2.shape easily,
# we convert them both to Python tuples.
assert tuple(array_1.shape) == tuple(array_2.shape)
result = np.zeros((x_max, y_max), dtype=DTYPE)
result_view: cython.int[:, :] = result
tmp: cython.int
x: cython.Py_ssize_t
y: cython.Py_ssize_t
for x in range(x_max):
for y in range(y_max):
tmp = clip(array_1[x, y], 2, 10)
tmp = tmp * a + array_2[x, y] * b
result_view[x, y] = tmp + c
return result
import numpy as np
DTYPE = np.intc
cdef int clip(int a, int min_value, int max_value):
return min(max(a, min_value), max_value)
def compute(int[:, :] array_1, int[:, :] array_2, int a, int b, int c):
cdef Py_ssize_t x_max = array_1.shape[0]
cdef Py_ssize_t y_max = array_1.shape[1]
# array_1.shape is now a C array, no it's not possible
# to compare it simply by using == without a for-loop.
# To be able to compare it to array_2.shape easily,
# we convert them both to Python tuples.
assert tuple(array_1.shape) == tuple(array_2.shape)
result = np.zeros((x_max, y_max), dtype=DTYPE)
cdef int[:, :] result_view = result
cdef int tmp
cdef Py_ssize_t x, y
for x in range(x_max):
for y in range(y_max):
tmp = clip(array_1[x, y], 2, 10)
tmp = tmp * a + array_2[x, y] * b
result_view[x, y] = tmp + c
return result
Let’s see how much faster accessing is now.
In [22]: %timeit compute_memview.compute(array_1, array_2, a, b, c)
22.9 ms ± 197 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)
Note the importance of this change. We’re now 3081 times faster than an interpreted version of Python and 4.5 times faster than NumPy.
Memoryviews can be used with slices too, or even with Python arrays. Check out the memoryview page to see what they can do for you.
Tuning indexing further¶
The array lookups are still slowed down by two factors:
Bounds checking is performed.
Negative indices are checked for and handled correctly. The code above is explicitly coded so that it doesn’t use negative indices, and it (hopefully) always access within bounds.
With decorators, we can deactivate those checks:
...
import cython
@cython.boundscheck(False) # Deactivate bounds checking
@cython.wraparound(False) # Deactivate negative indexing.
def compute(array_1: cython.int[:, :], array_2: cython.int[:, :],
a: cython.int, b: cython.int, c: cython.int):
...
...
cimport cython
@cython.boundscheck(False) # Deactivate bounds checking
@cython.wraparound(False) # Deactivate negative indexing.
def compute(int[:, :] array_1, int[:, :] array_2, int a, int b, int c):
...
Now bounds checking is not performed (and, as a side-effect, if you ‘’do’’ happen to access out of bounds you will in the best case crash your program and in the worst case corrupt data). It is possible to switch bounds-checking mode in many ways, see Compiler directives for more information.
In [23]: %timeit compute_index.compute(array_1, array_2, a, b, c)
16.8 ms ± 25.4 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
We’re faster than the NumPy version (6.2x). NumPy is really well written, but does not performs operation lazily, resulting in a lot of intermediate copy operations in memory. Our version is very memory efficient and cache friendly because we can execute the operations in a single run over the data.
Warning
Speed comes with some cost. Especially it can be dangerous to set typed
objects (like array_1, array_2 and result_view in our sample code) to None.
Setting such objects to None is entirely legal, but all you can do with them
is check whether they are None. All other use (attribute lookup or indexing)
can potentially segfault or corrupt data (rather than raising exceptions as
they would in Python).
The actual rules are a bit more complicated but the main message is clear: Do
not use typed objects without knowing that they are not set to None.
Declaring the NumPy arrays as contiguous¶
For extra speed gains, if you know that the NumPy arrays you are providing are contiguous in memory, you can declare the memoryview as contiguous.
We give an example on an array that has 3 dimensions. If you want to give Cython the information that the data is C-contiguous you have to declare the memoryview like this:
a: cython.int[:,:,::1]
cdef int [:,:,::1] a
If you want to give Cython the information that the data is Fortran-contiguous you have to declare the memoryview like this:
a: cython.int[::1, :, :]
cdef int [::1, :, :] a
If all this makes no sense to you, you can skip this part, declaring arrays as contiguous constrains the usage of your functions as it rejects array slices as input. If you still want to understand what contiguous arrays are all about, you can see this answer on StackOverflow.
For the sake of giving numbers, here are the speed gains that you should get by declaring the memoryviews as contiguous:
In [23]: %timeit compute_contiguous.compute(array_1, array_2, a, b, c)
11.1 ms ± 30.2 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
We’re now around nine times faster than the NumPy version, and 6300 times faster than the pure Python version!
Making the function cleaner¶
Declaring types can make your code quite verbose. If you don’t mind
Cython inferring the C types of your variables, you can use
the infer_types=True compiler directive at the top of the file.
It will save you quite a bit of typing.
Note that since type declarations must happen at the top indentation level,
Cython won’t infer the type of variables declared for the first time
in other indentation levels. It would change too much the meaning of
our code. This is why, we must still declare manually the type of the
tmp, x and y variable.
And actually, manually giving the type of the tmp variable will
be useful when using fused types.
# cython: infer_types=True
import numpy as np
import cython
DTYPE = np.intc
@cython.cfunc
def clip(a: cython.int, min_value: cython.int, max_value: cython.int) -> cython.int:
return min(max(a, min_value), max_value)
@cython.boundscheck(False)
@cython.wraparound(False)
def compute(array_1: cython.int[:, ::1], array_2: cython.int[:, ::1],
a: cython.int, b: cython.int, c: cython.int):
x_max = array_1.shape[0]
y_max = array_1.shape[1]
assert tuple(array_1.shape) == tuple(array_2.shape)
result = np.zeros((x_max, y_max), dtype=DTYPE)
result_view: cython.int[:, ::1] = result
tmp: cython.int
x: cython.Py_ssize_t
y: cython.Py_ssize_t
for x in range(x_max):
for y in range(y_max):
tmp = clip(array_1[x, y], 2, 10)
tmp = tmp * a + array_2[x, y] * b
result_view[x, y] = tmp + c
return result
# cython: infer_types=True
import numpy as np
cimport cython
DTYPE = np.intc
cdef int clip(int a, int min_value, int max_value):
return min(max(a, min_value), max_value)
@cython.boundscheck(False)
@cython.wraparound(False)
def compute(int[:, ::1] array_1, int[:, ::1] array_2, int a, int b, int c):
x_max = array_1.shape[0]
y_max = array_1.shape[1]
assert tuple(array_1.shape) == tuple(array_2.shape)
result = np.zeros((x_max, y_max), dtype=DTYPE)
cdef int[:, ::1] result_view = result
cdef int tmp
cdef Py_ssize_t x, y
for x in range(x_max):
for y in range(y_max):
tmp = clip(array_1[x, y], 2, 10)
tmp = tmp * a + array_2[x, y] * b
result_view[x, y] = tmp + c
return result
We now do a speed test:
In [24]: %timeit compute_infer_types.compute(array_1, array_2, a, b, c)
11.5 ms ± 261 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
Lo and behold, the speed has not changed.
More generic code¶
All those speed gains are nice, but adding types constrains our code.
At the moment, it would mean that our function can only work with
NumPy arrays with the np.intc type. Is it possible to make our
code work for multiple NumPy data types?
Yes, with the help of a new feature called fused types. You can learn more about it at this section of the documentation. It is similar to C++ ‘s templates. It generates multiple function declarations at compile time, and then chooses the right one at run-time based on the types of the arguments provided. By comparing types in if-conditions, it is also possible to execute entirely different code paths depending on the specific data type.
In our example, since we don’t have access anymore to the NumPy’s dtype
of our input arrays, we use those if-else statements to
know what NumPy data type we should use for our output array.
In this case, our function now works for ints, doubles and floats.
# cython: infer_types=True
import numpy as np
import cython
my_type = cython.fused_type(cython.int, cython.double, cython.longlong)
@cython.exceptval(check=False)
@cython.cfunc
def clip(a: my_type, min_value: my_type, max_value: my_type) -> my_type:
return min(max(a, min_value), max_value)
@cython.boundscheck(False)
@cython.wraparound(False)
def compute(array_1: my_type[:, ::1], array_2: my_type[:, ::1], a: my_type, b: my_type, c: my_type):
x_max = array_1.shape[0]
y_max = array_1.shape[1]
assert tuple(array_1.shape) == tuple(array_2.shape)
if my_type is cython.int:
dtype = np.intc
elif my_type is cython.double:
dtype = np.double
elif my_type is cython.longlong:
dtype = np.longlong
result = np.zeros((x_max, y_max), dtype=dtype)
result_view: my_type[:, ::1] = result
tmp: my_type
x: cython.Py_ssize_t
y: cython.Py_ssize_t
for x in range(x_max):
for y in range(y_max):
tmp = clip(array_1[x, y], 2, 10)
tmp = tmp * a + array_2[x, y] * b
result_view[x, y] = tmp + c
return result
# cython: infer_types=True
import numpy as np
cimport cython
ctypedef fused my_type:
int
double
long long
cdef my_type clip(my_type a, my_type min_value, my_type max_value):
return min(max(a, min_value), max_value)
@cython.boundscheck(False)
@cython.wraparound(False)
def compute(my_type[:, ::1] array_1, my_type[:, ::1] array_2, my_type a, my_type b, my_type c):
x_max = array_1.shape[0]
y_max = array_1.shape[1]
assert tuple(array_1.shape) == tuple(array_2.shape)
if my_type is int:
dtype = np.intc
elif my_type is double:
dtype = np.double
elif my_type is cython.longlong:
dtype = np.longlong
result = np.zeros((x_max, y_max), dtype=dtype)
cdef my_type[:, ::1] result_view = result
cdef my_type tmp
cdef Py_ssize_t x, y
for x in range(x_max):
for y in range(y_max):
tmp = clip(array_1[x, y], 2, 10)
tmp = tmp * a + array_2[x, y] * b
result_view[x, y] = tmp + c
return result
We can check that the output type is the right one:
>>> compute(array_1, array_2, a, b, c).dtype
dtype('int32')
>>> compute(array_1.astype(np.double), array_2.astype(np.double), a, b, c).dtype
dtype('float64')
We now do a speed test:
In [25]: %timeit compute_fused_types.compute(array_1, array_2, a, b, c)
11.5 ms ± 258 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
More versions of the function are created at compile time. So it makes sense that the speed doesn’t change for executing this function with integers as before.
Using multiple threads¶
Cython has support for OpenMP. It also has some nice wrappers around it,
like the function prange(). You can see more information about Cython and
parallelism in Using Parallelism. Since we do elementwise operations, we can easily
distribute the work among multiple threads. It’s important not to forget to pass the
correct arguments to the compiler to enable OpenMP. When using the Jupyter notebook,
you should use the cell magic like this:
%%cython --force
# distutils: extra_compile_args=-fopenmp
# distutils: extra_link_args=-fopenmp
For MSVC (on Windows) you should use /openmp instead of -fopenmp.
The GIL must be released (see Releasing the GIL), so this is why we
declare our clip() function nogil.
# distutils: extra_compile_args=-fopenmp
# distutils: extra_link_args=-fopenmp
import numpy as np
import cython
from cython.parallel import prange
my_type = cython.fused_type(cython.int, cython.double, cython.longlong)
# We declare our plain c function nogil
@cython.exceptval(check=False)
@cython.nogil
@cython.cfunc
def clip(a: my_type, min_value: my_type, max_value: my_type) -> my_type:
return min(max(a, min_value), max_value)
@cython.boundscheck(False)
@cython.wraparound(False)
def compute(array_1: my_type[:, ::1], array_2: my_type[:, ::1], a: my_type, b: my_type, c: my_type):
x_max: cython.Py_ssize_t = array_1.shape[0]
y_max: cython.Py_ssize_t = array_1.shape[1]
assert tuple(array_1.shape) == tuple(array_2.shape)
if my_type is cython.int:
dtype = np.intc
elif my_type is cython.double:
dtype = np.double
elif my_type is cython.longlong:
dtype = np.longlong
result = np.zeros((x_max, y_max), dtype=dtype)
result_view: my_type[:, ::1] = result
tmp: my_type
x: cython.Py_ssize_t
y: cython.Py_ssize_t
# We use prange here.
for x in prange(x_max, nogil=True):
for y in range(y_max):
tmp = clip(array_1[x, y], 2, 10)
tmp = tmp * a + array_2[x, y] * b
result_view[x, y] = tmp + c
return result
# distutils: extra_compile_args=-fopenmp
# distutils: extra_link_args=-fopenmp
import numpy as np
cimport cython
from cython.parallel import prange
ctypedef fused my_type:
int
double
long long
# We declare our plain c function nogil
cdef my_type clip(my_type a, my_type min_value, my_type max_value) noexcept nogil:
return min(max(a, min_value), max_value)
@cython.boundscheck(False)
@cython.wraparound(False)
def compute(my_type[:, ::1] array_1, my_type[:, ::1] array_2, my_type a, my_type b, my_type c):
cdef Py_ssize_t x_max = array_1.shape[0]
cdef Py_ssize_t y_max = array_1.shape[1]
assert tuple(array_1.shape) == tuple(array_2.shape)
if my_type is int:
dtype = np.intc
elif my_type is double:
dtype = np.double
elif my_type is cython.longlong:
dtype = np.longlong
result = np.zeros((x_max, y_max), dtype=dtype)
cdef my_type[:, ::1] result_view = result
cdef my_type tmp
cdef Py_ssize_t x, y
# We use prange here.
for x in prange(x_max, nogil=True):
for y in range(y_max):
tmp = clip(array_1[x, y], 2, 10)
tmp = tmp * a + array_2[x, y] * b
result_view[x, y] = tmp + c
return result
Note
Currently, Cython is checking whether there was a raised exception after every call of the function clip().
Checking a raised exception requires the GIL to be held which causes overhead inside a nogil loop.
The need to check here is a bug with functions returning a fused type (see #5586 for the details).
To avoid acquiring the GIL, the function is declared as noexcept or @cython.exceptval(check=False). See the Error return values section for more details.
We can have substantial speed gains for minimal effort:
In [25]: %timeit compute_prange.compute(array_1, array_2, a, b, c)
9.33 ms ± 412 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
We’re now 7558 times faster than the pure Python version and 11.1 times faster than NumPy!
Where to go from here?¶
If you want to learn how to make use of BLAS or LAPACK with Cython, you can watch the presentation of Ian Henriksen at SciPy 2015.
If you want to learn how to use Pythran as backend in Cython, you can see how in Pythran as a NumPy backend. Note that using Pythran only works with the old buffer syntax and not yet with memoryviews.
